强化学习核心概念与算法解析 (Reinforcement Learning Core Concepts and Algorithms Explained)
强化学习核心概念与算法解析
摘要
大型语言模型(LLM)的卓越能力,很大程度上归功于强化学习技术的应用,特别是基于人类反馈的强化学习(Reinforcement Learning from Human Feedback, RLHF)。然而,在开源社区中,强化学习的普及度远不及监督微调(Supervised Fine-Tuning, SFT)。本文旨在系统性地梳理强化学习的基础理论、核心概念及关键算法,从基本定义出发,逐步深入到马尔可夫决策过程(MDP)、Q-Learning,最终延伸至深度Q网络(DQN),为理解并应用强化学习于语言模型领域奠定坚实的理论基础。
本文是我个人的学习总结,如果存在错误或需要更新,可以随时通过我的联系方式与我联系指正。
1. 引言
1.1 背景
近年来,基于人类反馈的强化学习(RLHF)已成为优化大型语言模型(LLM)性能的关键技术。尽管其效果显著,但与监督学习方法相比,强化学习在实践中的应用仍面临诸多挑战。主要原因有二:
- 数据获取难度:RLHF 依赖于高质量的人类偏好数据,其收集与标注成本高昂。
- 技术壁垒:多数从业者对监督学习更为熟悉,而对强化学习的理论和实践相对陌生,这限制了其在项目中的应用。
本文旨在消除这一知识鸿沟,帮助读者建立对强化学习的系统性认知。
1.2 本文目标
本文将通过循序渐进的方式,构建一个关于强化学习的完整知识框架:
- 从强化学习的基本定义和核心思想入手。
- 深入探讨在语言模型微调中广泛应用的 RLHF 关键算法。
- 最终证明,强化学习的理念在实践中易于理解和应用。
注:在本文中,术语“智能体(agent)”将用于指代需要进行微调的语言模型。
2. 机器学习范式对比
2.1 监督学习 (Supervised Learning)
在监督学习中,数据集由输入序列及其对应的“正确”标签组成。模型训练的目标是学习从输入到标签的映射关系。
以文本分类为例,微调一个BERT模型以识别不当言论,其训练流程如下:
- 从数据集中采样一个微批次(mini-batch)。
- 模型根据输入预测标签。
- 计算损失(如交叉熵损失)。
- 反向传播梯度。
- 更新模型权重。
2.2 自监督学习 (Self-Supervised Learning)
自监督学习的流程与监督学习相似,但其“标签”来源于数据自身,无需人工标注。例如,语言模型的预训练任务通常是预测序列中的下一个词元(token),而这个词元本身就存在于原始文本中。
2.3 强化学习 (Reinforcement Learning, RL)
强化学习适用于需要模型通过与环境的交互和反馈进行学习的场景。与依赖固定标签的监督学习不同,强化学习通过“试错”机制进行训练:模型产生一个输出,接收一个代表反馈的“奖励(reward)”,并根据该奖励调整自身行为。
在语言模型的 RLHF 场景中,模型生成一段文本,人类评估其质量并给出一个分数(即奖励)。模型利用这个分数来优化其策略,以期在未来生成更高质量的输出。

3. 强化学习工作原理
3.1 为何需要强化学习?
在 RLHF 中,人类的偏好评分是主观的,无法表示为一个可微分的数学函数。因此,我们不能像监督学习那样,直接通过人类的判断来计算梯度并反向传播。人类反馈在此充当了一个“黑箱”,我们只知其结果(得分),却无法直接利用它来指导模型的参数更新。
注:在传统的强化学习环境中,环境本身是不可微分的。然而,在LLM的微调中,奖励通常由一个可微分的奖励模型(Reward Model)提供,这使得端到端的监督式训练成为可能(例如,直接偏好优化 DPO)。但若奖励直接由人类提供,则必须依赖强化学习方法。
3.2 强化学习的有效性
强化学习的优势在于它能够处理不可微分的反馈信号。无论是来自人类、规则系统还是其他模型的评分,只要能提供一个标量奖励,我们就能训练语言模型。这使得我们可以根据期望的目标(如更有用、更安全、更诚实)来塑造模型的行为。
4. 强化学习的核心构成
4.1 基本结构
强化学习问题通常遵循一个通用结构:智能体(Agent) 在特定 状态(State) 下,执行一个 动作(Action),与 环境(Environment) 发生交互,并接收一个 奖励(Reward)。
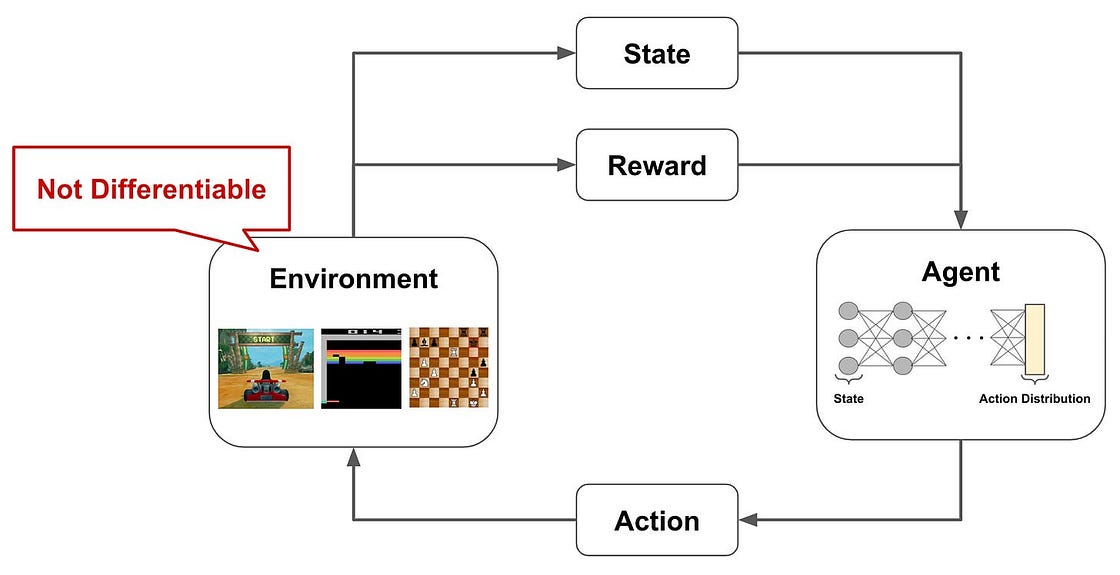
智能体的动作会改变环境的状态,其最终目标是学习一个能最大化长期累积奖励的策略。在许多场景中,奖励是延迟的,需要一系列正确的动作才能获得,这被称为“长奖励周期(long reward horizon)”。
4.2 马尔可夫决策过程 (Markov Decision Process, MDP)
为了更形式化地描述强化学习,我们引入马尔可夫决策过程(MDP)。MDP为智能体与环境的交互提供了一个数学框架,包含以下核心要素:
状态(States, S): 智能体可能所处的不同情况。
动作(Actions, A): 智能体在每个状态下可以做出的选择。
奖励(Rewards, R): 执行动作后收到的反馈信号。
状态转移(Transitions, P): 在某个状态执行一个动作后,转移到下一个状态的规则。
策略(Policy, π): 智能体的行为准则,即从状态到动作的映射。
策略函数 (π(a|s)): 输入当前状态
s,输出一个关于可用动作a的概率分布。状态转移函数 (P(s’|s, a)): 输入当前状态
s和动作a,输出环境转移到下一个状态s'的概率。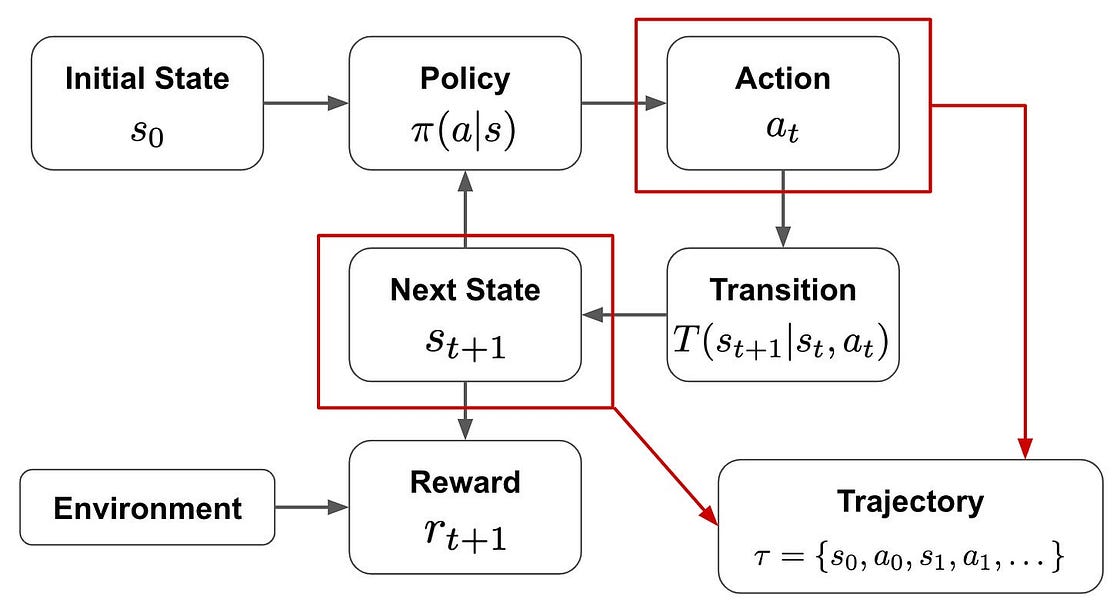
4.3 智能体、策略与回报 (Return)
- 智能体 vs. 策略: 智能体是在环境中执行操作的实体,而策略是智能体用来决策的“大脑”或“战略”。我们的目标是学习一个最优策略,以指导智能体获得最大化的长期回报。
- 轨迹 (Trajectory): 智能体与环境交互产生的一系列状态、动作和奖励的序列
(s₀, a₀, r₁, s₁, a₁, r₂, ...)。 - 回报 (Return, G): 一条轨迹上所有奖励的总和。为了平衡短期与长期利益,未来的奖励会通过一个折扣因子
γ(gamma) 进行衰减。
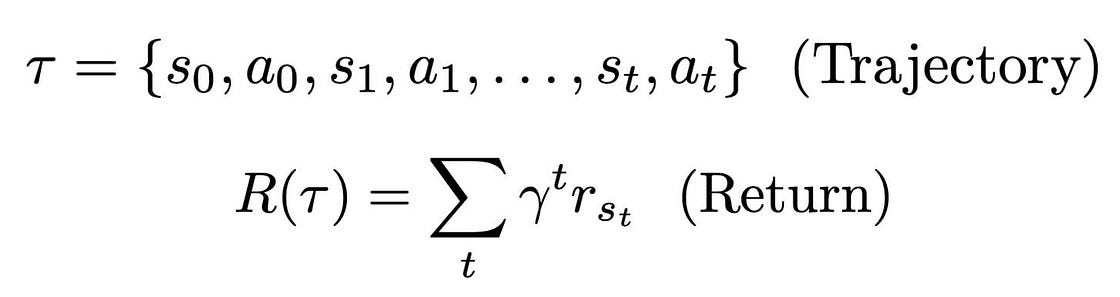
强化学习的核心目标是训练一个智能体,使其遵循一个能最大化期望回报的策略。
4.4 关键术语
- 回合 (Episode): 从初始状态开始,到终止状态结束的一次完整的交互过程。
- 折扣因子 (Discount Factor, γ): 衡量未来奖励当前价值的系数,取值范围为
[0, 1]。γ越小,智能体越关注短期奖励;γ越大,则越重视长期回报。 - 同策略 (On-Policy) vs. 异策略 (Off-Policy):
- 同策略: 用于生成动作的策略与用于评估和改进的策略是同一个。
- 异策略: 用于生成动作的“行为策略”与用于评估和改进的“目标策略”不同。
- ε-贪心策略 (ε-Greedy Policy): 一种平衡探索(Exploration)与利用(Exploitation)的策略。智能体以
1-ε的概率选择当前最优动作(利用),以ε的概率随机选择一个动作(探索)。
5. Q-Learning 算法
Q-Learning 是强化学习中的一种经典无模型(model-free)算法,它为我们理解RL算法的工作方式提供了一个很好的起点。
5.1 什么是 Q-Learning?
Q-Learning 的核心思想是学习一个名为 Q函数 (Q-function) 的动作价值函数。Q函数 Q(s, a) 用于估计在状态 s 下执行动作 a,并在此后遵循某个策略所能获得的期望回报。
在Q-Learning中,我们使用一个 Q表 (Q-table) 来存储每个状态-动作对的Q值。算法开始时,Q表被初始化为零。随着智能体与环境的交互,它会根据贝尔曼方程(Bellman Equation)不断更新Q表中的值。
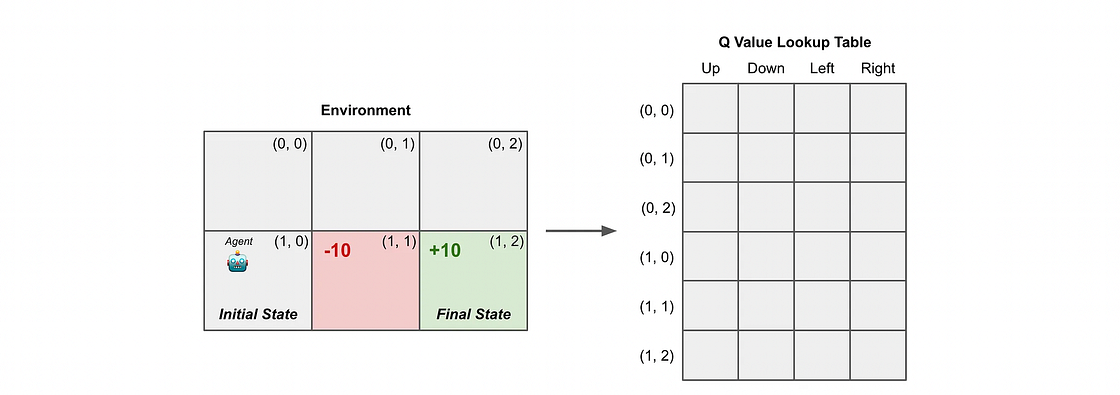
5.2 Q-Learning 算法流程
Q-Learning 算法的执行步骤如下:
- 初始化Q表为全零。
- 对于每个回合:
a. 选择一个初始状态
s。 b. 只要未达到终止状态: i. 在当前状态s,使用 ε-贪心策略选择一个动作a。 ii. 执行动作a,从环境中观测到奖励r和新状态s'。 iii. 根据贝尔曼方程更新Q值:Q(s, a) ← Q(s, a) + α * [r + γ * max_a'(Q(s', a')) - Q(s, a)]其中α是学习率。 iv. 更新状态:s ← s'。
Q-Learning 是一种异策略算法,因为它在选择动作时使用 ε-贪心策略(行为策略),但在更新Q值时使用了贪心策略(max_a' Q(s', a')),即假设在下一个状态会选择最优动作(目标策略)。
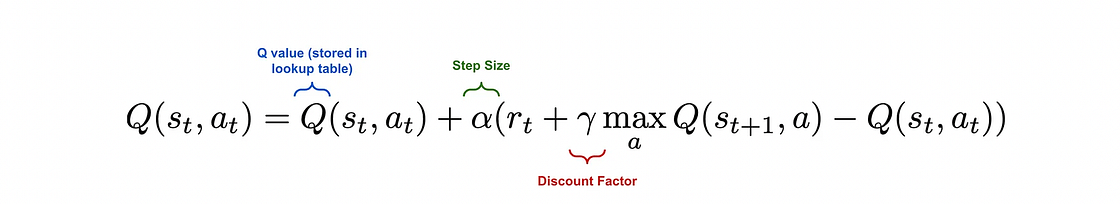
5.3 Q-Learning 代码示例
下面是一个简单的Q-Learning实现,用于直观理解其工作原理。
import numpy as np
# 定义环境参数
n_states = 16 # 状态数量
n_actions = 4 # 动作数量
goal_state = 15 # 目标状态
Q_table = np.zeros((n_states, n_actions)) # 初始化Q表
# 设置超参数
learning_rate = 0.8 # 学习率
discount_factor = 0.95 # 折扣因子
exploration_prob = 0.2 # 探索概率
epochs = 1000 # 训练回合数
# Q-Learning 算法实现
for epoch in range(epochs):
current_state = np.random.randint(0, n_states) # 随机选择一个初始状态
while current_state != goal_state:
# 使用ε-贪心策略选择动作
if np.random.rand() < exploration_prob:
action = np.random.randint(0, n_actions) # 探索:随机选择动作
else:
action = np.argmax(Q_table[current_state]) # 利用:选择Q值最高的动作
# 模拟环境的响应
next_state = (current_state + 1) % n_states # 简化的状态转移
reward = 1 if next_state == goal_state else 0 # 到达目标则给予奖励
# 使用贝尔曼方程更新Q值
old_value = Q_table[current_state, action]
next_max = np.max(Q_table[next_state])
new_value = old_value + learning_rate * (reward + discount_factor * next_max - old_value)
Q_table[current_state, action] = new_value
current_state = next_state
print("训练后的Q表:")
print(Q_table)
# 观察Q表,可以看到接近目标状态(state 15)的Q值更高,
# 这表明智能体学习到了通往目标的最优路径。
6. 深度 Q-Learning (DQN)
6.1 从 Q-Learning 到 DQN
Q-Learning 的一个主要局限是Q表的大小。在状态和动作空间非常大(甚至是连续的)环境中,如视频游戏或现实世界任务,维护一个巨大的Q表是不现实的。
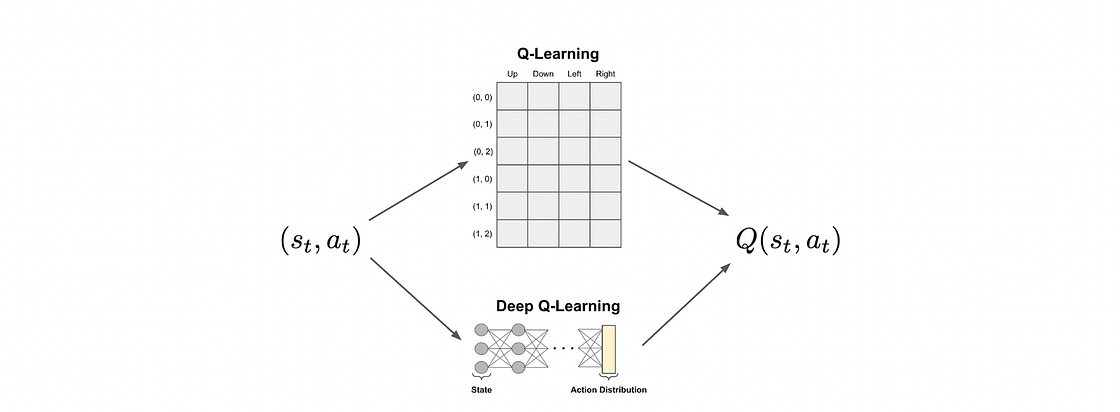
深度Q网络 (Deep Q-Network, DQN) 通过使用深度神经网络来近似Q函数,解决了这一问题。DQN不再存储每个状态-动作对的Q值,而是训练一个网络,该网络接收状态作为输入,并输出所有可能动作的Q值。
[图片]: DQN 结构示意图
6.2 DQN 算法
DQN 引入了两个关键技术来稳定训练过程:
经验回放 (Experience Replay): 智能体与环境交互产生的经验
(s, a, r, s')被存储在一个固定大小的缓冲区(Replay Buffer)中。在训练时,从缓冲区中随机采样小批量数据来更新网络,这打破了数据之间的相关性,使训练更稳定。目标网络 (Target Network): DQN 使用两个结构相同的神经网络:Q网络 和 目标网络。
- Q网络: 用于在每个步骤预测Q值,并进行频繁的更新。
- 目标网络: 用于计算贝尔曼方程中的目标Q值
(r + γ * max_a' Q_target(s', a'))。目标网络的权重是定期从Q网络复制而来,并在一段时间内保持固定。
DQN 训练流程:
- 智能体使用当前的Q网络和ε-贪心策略与环境交互,并将经验存入经验回放缓冲区。
- 从缓冲区中随机采样一批经验。
- 对于每个样本,使用Q网络计算预测Q值,使用目标网络计算目标Q值。
- 计算两者之间的均方误差(MSE)损失。
- 通过反向传播更新Q网络的权重。
- 每隔一定步数,将Q网络的权重复制到目标网络。
6.3 目标网络的作用
如果在计算目标Q值时也使用正在更新的Q网络,会导致目标值不断变化,使得训练过程像是在“追逐一个移动的目标”,非常不稳定。引入一个固定的目标网络可以提供一个稳定的学习目标,从而大大提高训练的稳定性。
6.4 DQN 基础代码框架
以下是DQN智能体的一个基本实现框架,展示了其核心组件。
# 假设已导入TensorFlow/Keras或PyTorch
# from tensorflow.keras.models import Sequential
# from tensorflow.keras.layers import Dense
# from tensorflow.keras.optimizers import Adam
class DQNAgent:
def __init__(self, state_size, action_size):
self.n_actions = action_size
# 定义超参数
self.lr = 0.001
self.gamma = 0.99
self.exploration_proba = 1.0
self.exploration_proba_decay = 0.005
self.batch_size = 32
# 经验回放缓冲区
self.memory_buffer = list()
self.max_memory_buffer = 2000
# 创建Q网络
self.model = self._build_model(state_size, action_size)
def _build_model(self, state_size, action_size):
# 使用Keras构建一个简单的全连接神经网络
model = Sequential([
Dense(units=24, input_dim=state_size, activation='relu'),
Dense(units=24, activation='relu'),
Dense(units=action_size, activation='linear')
])
model.compile(loss="mse", optimizer=Adam(lr=self.lr))
return model
def compute_action(self, current_state):
# ε-贪心策略
if np.random.uniform(0, 1) < self.exploration_proba:
return np.random.choice(range(self.n_actions))
q_values = self.model.predict(current_state)[0]
return np.argmax(q_values)
def store_episode(self, current_state, action, reward, next_state, done):
# 存储经验
self.memory_buffer.append({
"current_state": current_state,
"action": action,
"reward": reward,
"next_state": next_state,
"done": done
})
if len(self.memory_buffer) > self.max_memory_buffer:
self.memory_buffer.pop(0)
def train(self):
# 从缓冲区采样
np.random.shuffle(self.memory_buffer)
batch_sample = self.memory_buffer[0:self.batch_size]
for experience in batch_sample:
# 预测当前状态的Q值
q_current_state = self.model.predict(experience["current_state"])
# 计算目标Q值
q_target = experience["reward"]
if not experience["done"]:
# 注意:一个完整的DQN实现会在这里使用目标网络
q_target = q_target + self.gamma * np.max(self.model.predict(experience["next_state"])[0])
q_current_state[0][experience["action"]] = q_target
# 训练模型
self.model.fit(experience["current_state"], q_current_state, verbose=0)
def update_exploration_probability(self):
# 更新探索概率
self.exploration_proba *= np.exp(-self.exploration_proba_decay)
7. 结论与展望
本文从强化学习的基本概念出发,系统介绍了其与监督学习的差异、核心构成要素(MDP),并详细阐述了两种关键算法:Q-Learning 和深度Q网络(DQN)。
尽管DQN非常高效,但仍有改进空间。例如,使用同一个网络来选择动作和评估价值会导致高估问题(Maximization Bias)。此外,随机从经验回放缓冲区中采样可能不是最优策略,优先处理TD误差较大的经验(Prioritized Experience Replay)可能会带来更好的效果。后续的算法如Double DQN、Dueling DQN等正是为了解决这些问题而提出的。